Sphere Impact with Rod - Exploring Contact Penetration

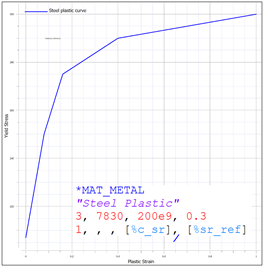
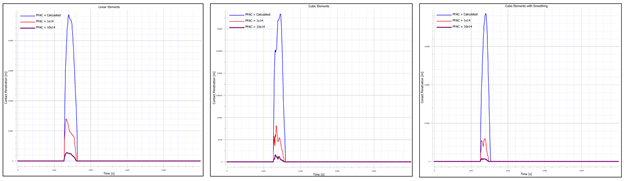
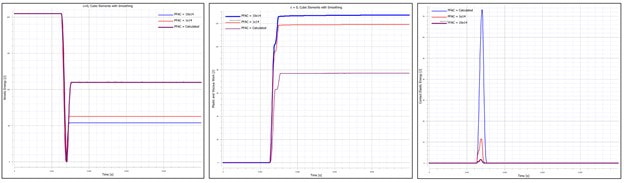
     In this discussion, we will be exploring concepts in energy and momentum conservation using as an example the collision of a sphere with a rigid bar. As usual, these models are built in the IMPETUS Afea Solver and are meant to explore simple concepts in mechanics, in addition to things to keep in mind when performing analysis of larger systems and models. 
     This model consists of a deformable steel sphere impacting a rigid, steel bar. The steel bar is constrained in XYZ translation and XYZ rotation and the sphere is constrained in XY translation using *BC_MOTION. The sphere is given an initial velocity of -10 m/s using *INITIAL_VELOCITY. Contact is defined between the sphere and the bar using *CONTACT. Friction is not considered in the contact interface. Penalty stiffness at the contact interface is  is explored and is varied between the calculated value of 0.1e14, 1e14, and 10e14. The impact model setup is shown in Figure 1. 

Figure 1. Model setup for sphere impacting rigid bar.

      The sphere is modeled with *MAT_METAL in order to capture plastic deformation during the collision. The yield stress vs. plastic strain curve is shown in Figure 2. Strain rate hardening was not considered in this model.  

Figure 2. Yield stress vs. plastic strain for *MAT_METAL steel curve. Note stress is in Mpa.

For this two body system, we can write the coefficient restitution for the collision as:

     If both objects are rigid and kinetic energy is conserved, the coefficient of restitution would be equal to 1 and the initial and final velocity of the sphere would be equal and opposite. In reality, however, some energy is lost during the collision due to deformation, contact, etc. and the coefficient of restitution will be less than 1, indicating that some kinetic energy of the sphere is lost (final velocity less than initial velocity).
     In this study, the effect of penalty stiffness and element order/smoothing on the response of the sphere during and after impact will be explored. In IMPETUS, element order and smoothing is easily modified using the commands *CHANGE_P-ORDER and *SMOOTH_MESH, which apply the changes at runtime. Figure 3 contains images of the mesh for the three cases (linear elements, cubic elements, and cubic elements with smoothing). Note that smoothing removes element facets (or sharp corners), which could also be achieved by using a larger number of linear elements as well. Increasing mesh density and quadratic elements were not explored in this study. 

Figure 3. Linear, cubic, and cubic smoothed mesh for sphere collision model.

  ​     In models that involve contact, it is important to check contact penetration and ensure that its value is reasonable. In reality, tuning a numerical model properly requires physical test data to compare and validate against. There are many parameters that can be used to validate the model and it is up to the analyst to determine the most influential factors. What is clear, however, is that many parameters can affect the response of a model, so it is wise not to trust results without exploring what they mean and what their sensitivities are.
     Table 1 outlines the cases run for this study. Penalty stiffness factors of 0.1e14, 1e14, and 10e14 were used in conjunction with linear elements, cubic elements, and cubic elements with smoothing applied. The maximum contact penetration for each case is also shown. Maximum contact penetration for linear elements, cubic elements, and cubic elements with smoothing is visually shown in Figure 4.

Table 1. Outline of cases run in this study, including values for element order, smoothing, penalty stiffness, and contact penetration.

Figure 4. Contact penetration for linear elements, cubic elements, and cubic elements with smoothing.

Figure 5 contains the final velocity of the sphere as a function of time for each of the three cases. Figure 6 contains the kinetic energy, plastic energy, and contact elastic energy as a function of time for each of the three cases. 
​    From the plots, it can be seen that the contact penetration decreases as the element order is increased, when smoothing is introduced, and when the penalty stiffness is increased. What is of importance in this data is not necessarily the absolute values, but the fact that modifications to penalty stiffness and element order and/or mesh smoothing can affect the contact behavior and should be considered when analyzing larger systems and models.
     The differences in contact penetration as a result of changes in penalty stiffness can also be observed in the macro-response of the system, primarily in the form of energy transfer. The primary metric of interest is the final velocity of the sphere, however, plastic energy, kinetic energy, and contact elastic energy are also explored. Table 2 contains the three cases run using cubic elements and smoothing, but varying penalty stiffness factors.  Figure 5 contains the final velocity of the sphere as a function of time for each of the three cases and Figure 6 contains the kinetic energy, plastic energy, and contact elastic energy as a function of time for each of the three cases. 

Table 2. Three cases run with cubic elements and smoothing, including penalty stiffness and final velocity of the sphere.

Figure 5. Final velocity of sphere as function of time for varying penalty stiffness.

Figure 6. Kinetic energy, plastic energy, contact elastic energy for varying penalty stiffness.

     As can be observed, an increase in the penalty stiffness results in a decrease in velocity and a thus a decrease in kinetic energy. Simultaneously, the plastic energy increases and the contact elastic energy decreases. As in most problems, energy is conserved from its initial to final state and is, as a result, transformed to and from various forms – in this case from elastic energy and kinetic energy to plastic energy. The contact algorithm in IMPETUS uses the penalty method, which essentially implements a stiff spring between the interfaces to resist penetration. A spring has an energy that varies directly with stiffness and the square of displacement and a force that varies directly with stiffness and directly with displacement. As a result, as the penalty stiffness is increased, the contact penetration decreases (stiffer spring means less deflection for a given force) leading to a similar decrease in contact elastic energy. Furthermore, as the penalty stiffness increases, the stiffness of the interface increases leading to a larger amount of energy lost to plastic deformation of the sphere. This increase in plastic energy similarly reduces the kinetic energy and resulting final velocity, as observed.
     While the phenomenon observed make physical and numerical sense, their primary purpose in this study is to demonstrate trends and the sensitivity of a system’s response to changes in single parameters in order to highlight the fact that care must be taken when tuning a finite element model. Ideally, one has additional information in the form of test data or macro properties that can be used to properly validate the system response.       Contact penetration, however, should always be checked and additional parameters likely need to be tuned as well. Of great importance is typically the material model. As stated before, garbage in = garbage out, and one of the largest sources of error can come from an inaccurate material model.
​     The primary purpose of this study was to demonstrate the importance of checking contact penetration and in understanding how changes in small parameters can affect the global response of a model. In simple models, it may be straightforward to determine the largest source of error, however, when analyzing larger systems, these small things become very important to check.